
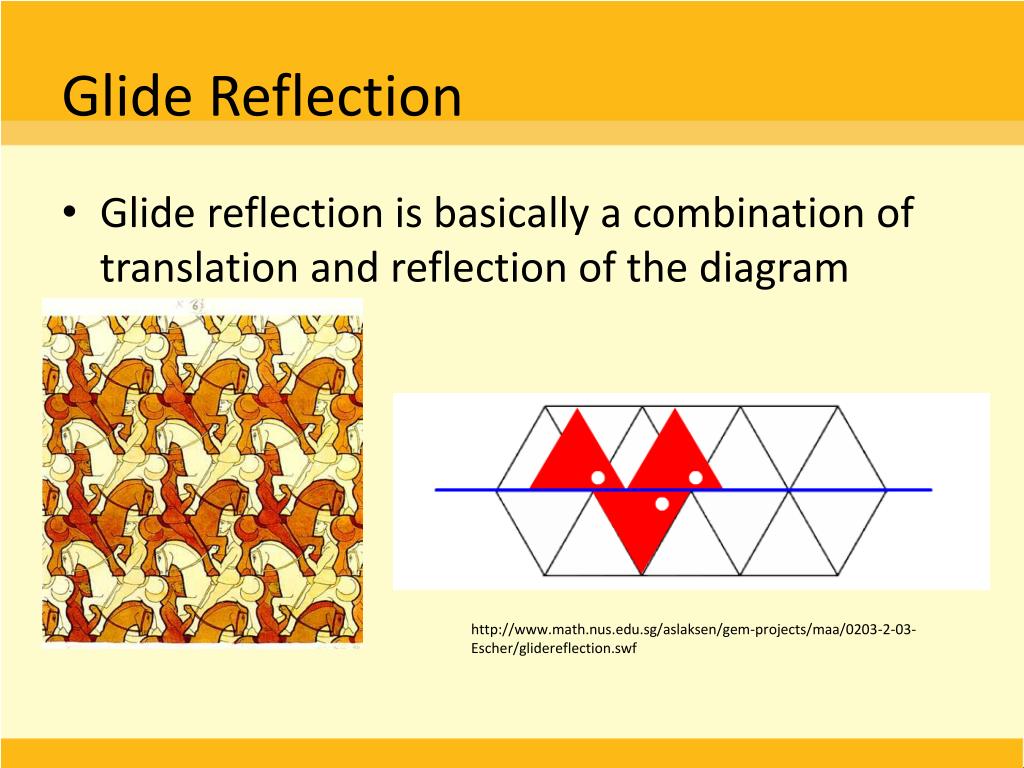
6 (glide-reflections, translations and rotations) is generated by a glide reflection and a rotation about a point on the line of reflection. If that is all it contains, this type is frieze group p11g.Įxample pattern with this symmetry group:įrieze group nr. In the case of glide reflection symmetry, the symmetry group of an object contains a glide reflection, and hence the group generated by it. Ĭombining two equal glide reflections gives a pure translation with a translation vector that is twice that of the glide reflection, so the even powers of the glide reflection form a translation group. The isometry group generated by just a glide reflection is an infinite cyclic group. This isometry maps the x-axis to itself any other line which is parallel to the x-axis gets reflected in the x-axis, so this system of parallel lines is left invariant. These are the two kinds of indirect isometries in 2D.įor example, there is an isometry consisting of the reflection on the x-axis, followed by translation of one unit parallel to it. Thus the effect of a reflection combined with any translation is a glide reflection, with as special case just a reflection. However, a glide reflection cannot be reduced like that. The combination of a reflection in a line and a translation in a perpendicular direction is a reflection in a parallel line. It can also be given a Schoenflies notation as S 2∞, Coxeter notation as, and orbifold notation as ∞×. A glide reflection can be seen as a limiting rotoreflection, where the rotation becomes a translation. In group theory, the glide plane is classified as a type of opposite isometry of the Euclidean plane.Ī single glide is represented as frieze group p11g. The intermediate step between reflection and translation can look different from the starting configuration, so objects with glide symmetry are in general, not symmetrical under reflection alone. In 2-dimensional geometry, a glide reflection (or transflection) is a symmetry operation that consists of a reflection over a line and then translation along that line, combined into a single operation. The operation of a glide reflection: A composite of a reflection across a line and a translation parallel to the line of reflection Since this footprint trail has glide reflection symmetry, applying the operation of glide reflection will map each left footprint into a right footprint and each right footprint to a left footprint, leading to a final configuration which is indistinguishable from the original. ( December 2016) ( Learn how and when to remove this template message) Please help improve it to make it understandable to non-experts, without removing the technical details.
This article may be too technical for most readers to understand.


 0 kommentar(er)
0 kommentar(er)
